Dual Quaternion Interpolation in Unity

Overview

This repo discusses two possible ways to interpolate rigid body motions in Unity.

The scripts were tested in Unity v2020.3.f25f1.

Independent SLERP + LERP Interpolation

In Unity, coordinate frames or poses are represented by Quaternion (representing rotation), and Vector3 (representing translation).

Each component (rotation or translation) has its respective interpolation method implemented out-of-the-box in Unity, to transition smoothly from one pose to another. Namely, they are Quarternion.Slerp for interpolating rotations and Vector3.Lerp for interpolating translations.

One direct way to interpolate rigid body motion in SE(3)\mathbb{SE(3)} is to interpolate two distinct poses independently in their rotation and translation component.

Figure 1 - Independent SLERP + LERP interpolation.

The code snippet below (from MoveIndependent.cs) shows how to achieve this rigid body motion interpolation with built-in Unity functionalities.

public class MoveIndependent : MonoBehaviour
{
    Quaternion startRotation;
    Quaternion endRotation;
    Vector3 startPosition;
    Vector3 endPosition;
    LineRenderer lr0;

    int totalFrames = 50*10;
    int counter;

    // Start is called before the first frame update
    void Start()
    {
        lr0 = new GameObject().AddComponent<LineRenderer>();
        lr0.gameObject.transform.SetParent(transform);
        lr0.gameObject.transform.SetPositionAndRotation(Vector3.zero, Quaternion.identity);

        startRotation = Quaternion.Euler(0f, 0f, 0f);
        startPosition = Vector3.zero;

        endPosition = new Vector3(-10f, 10f, 10f);
        endRotation = Quaternion.Euler(180f,0f,0f);

        counter = 0;

        transform.position = startPosition;
        transform.rotation = startRotation;
    }

    private void FixedUpdate() {
        if (counter < totalFrames) {
            counter += 1;
            // interpolation
            transform.rotation = Quaternion.Slerp(startRotation, endRotation, (float)counter / totalFrames);
            transform.position = Vector3.Lerp(startPosition, endPosition, (float) counter / totalFrames);

            // visualization
            List<Vector3> line0 = new List<Vector3> { startPosition, endPosition };
            lr0.startWidth = 0.1f;
            lr0.endWidth = 0.1f;
            lr0.SetPositions(line0.ToArray());
        }
        
    }
}

Full script: MoveIndependent.cs

Screw Linear Interpolation (ScLERP) with Dual Quaternions

Alternatively, one can interpolate rigid body motion between two poses along a screw motion as illustrated below:

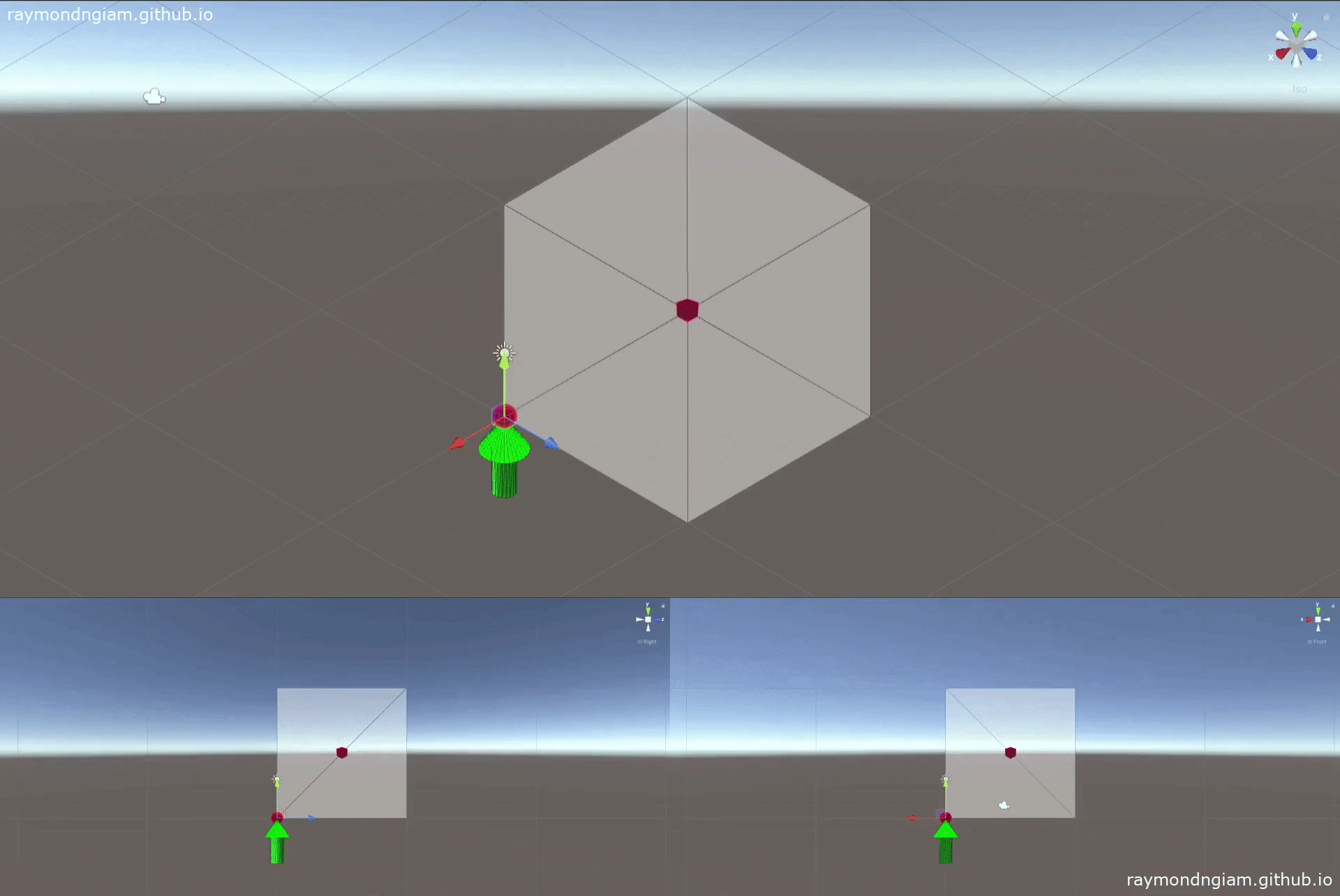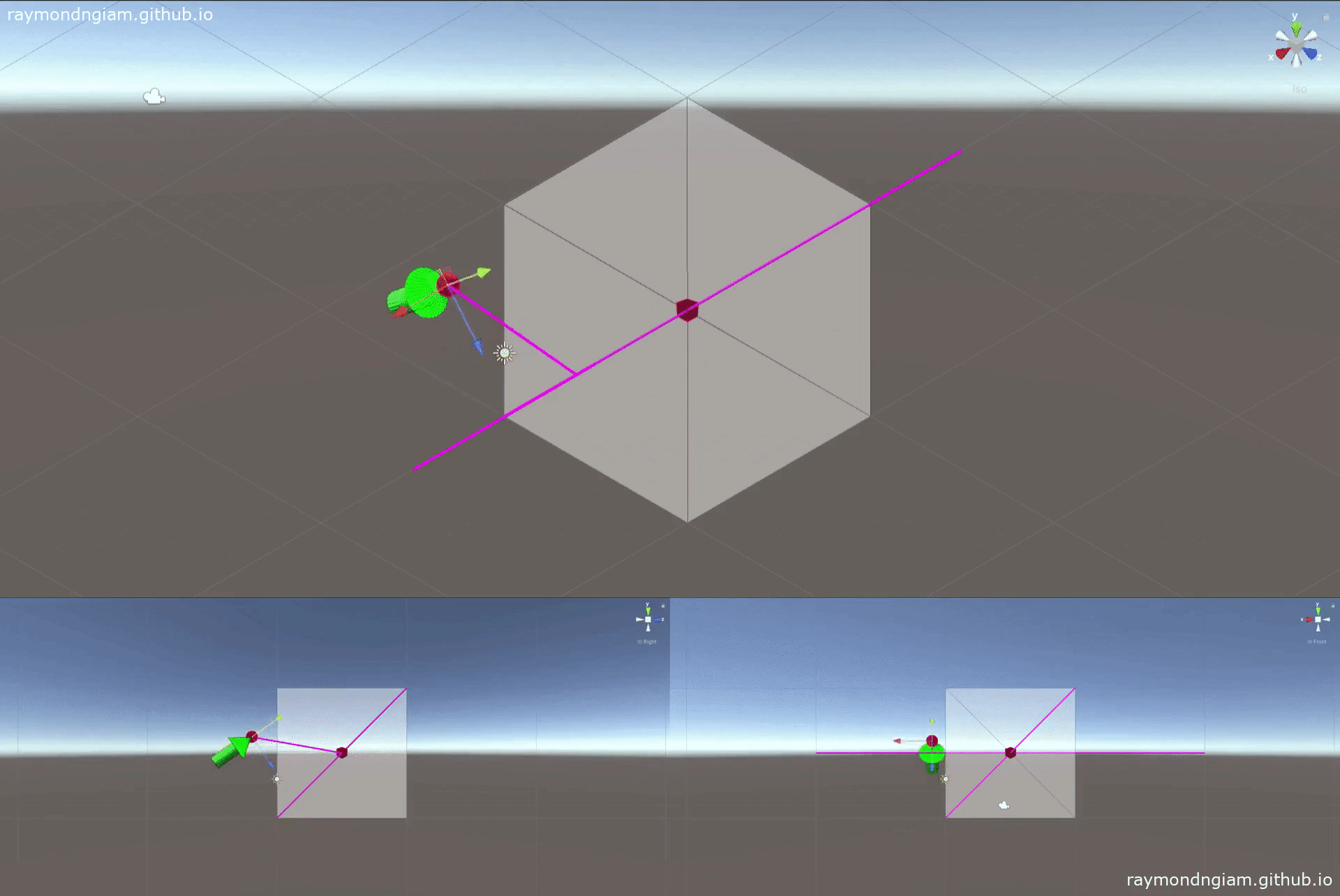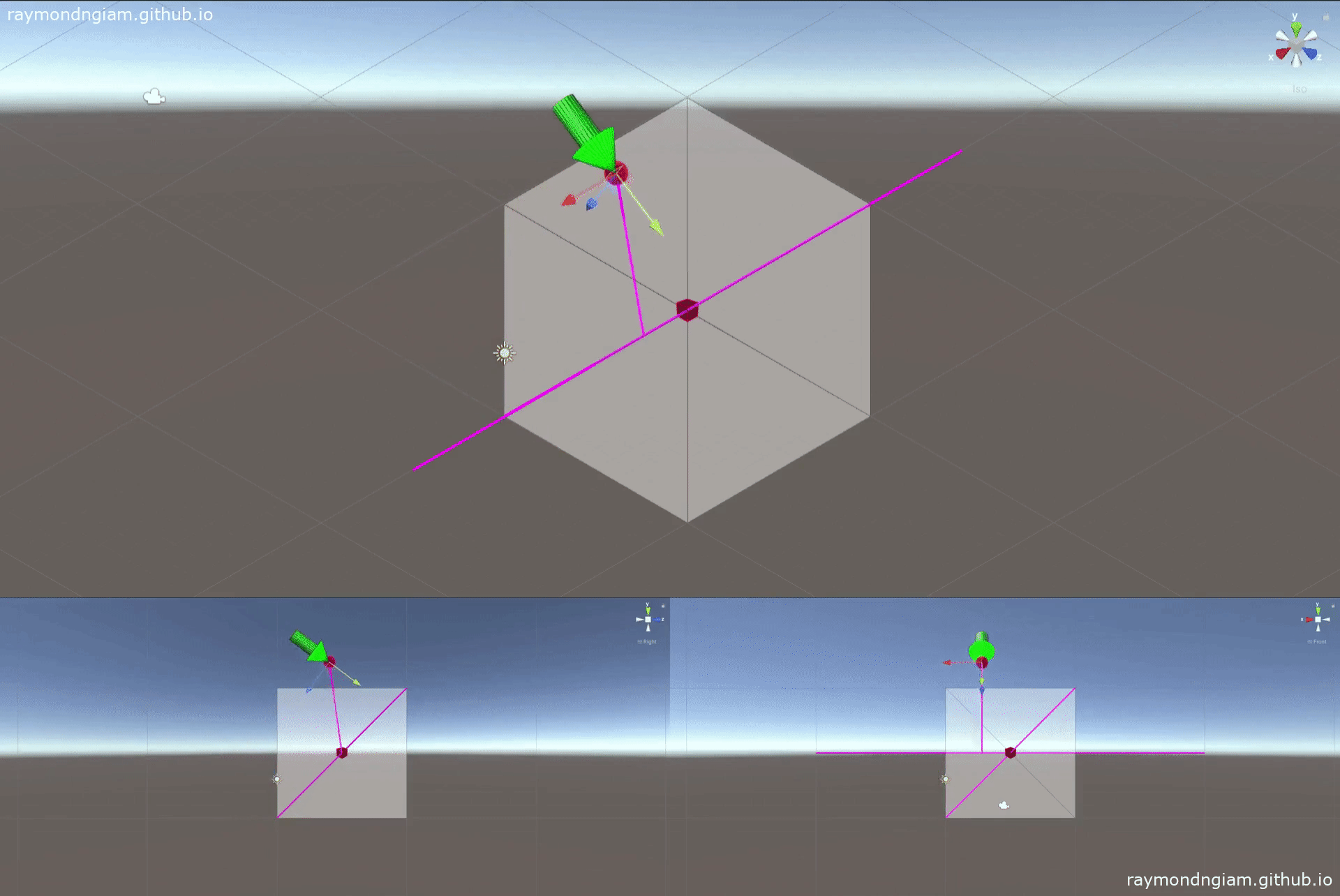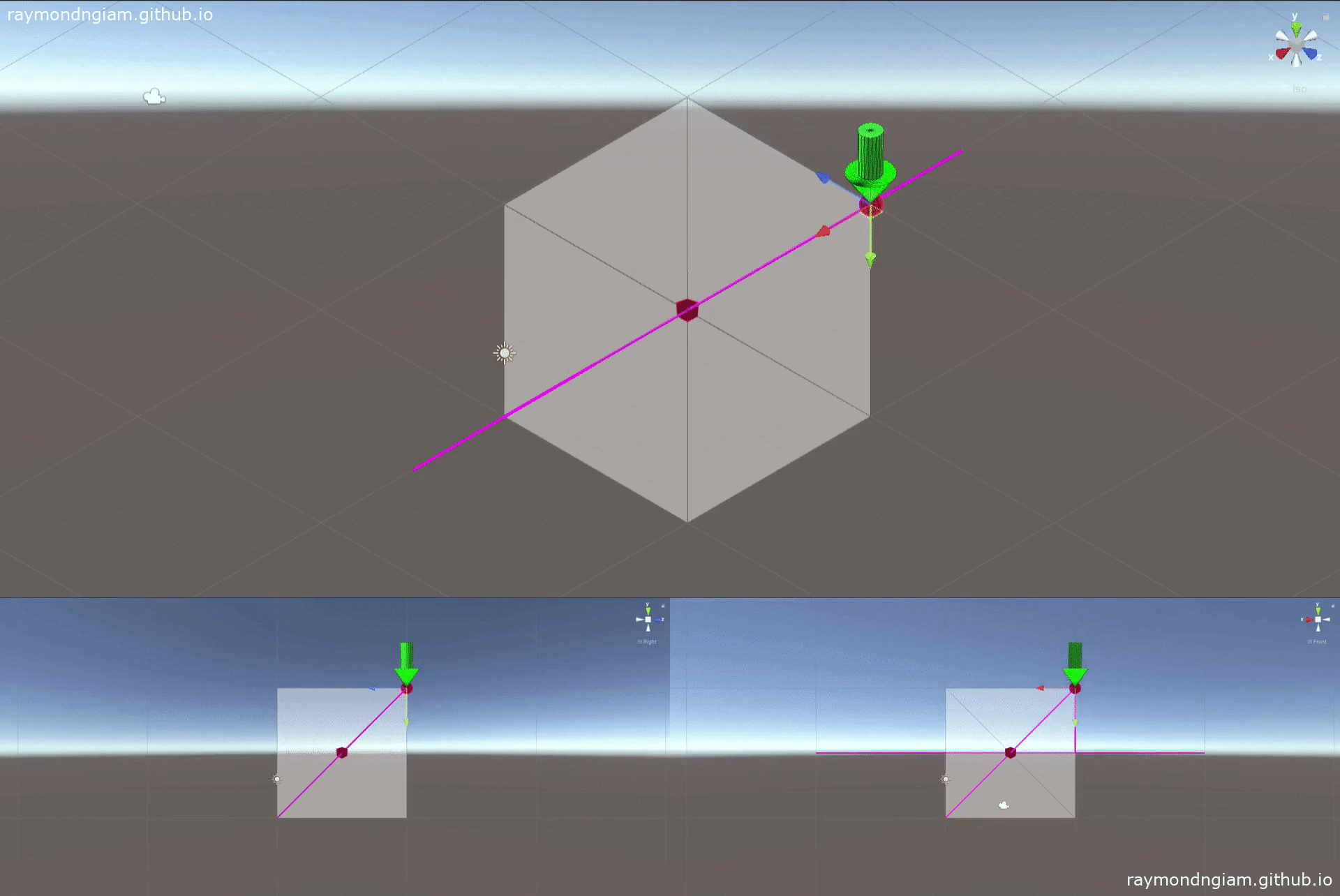
Figure 2 - Top: Perspective view of a screw motion. Lower left: Coaxial view of a screw motion. Lower right: Side view of a screw motion.

The code snippet below (from MoveDQ.cs) shows how to achieve this rigid body motion interpolation using a custom defined class DualQuat (which implementation is also defined in MoveDQ.cs).

public class MoveDQ : MonoBehaviour
{
    Quaternion startRotation;
    Quaternion endRotation;
    Vector3 startPosition;
    Vector3 endPosition;
    DualQuat startDQ;
    DualQuat endDQ;
    LineRenderer lr0;
    LineRenderer lr1;
    LineRenderer lr2;

    int totalFrames = 50*10;
    int counter;

    // Start is called before the first frame update
    void Start() {
        lr0 = new GameObject().AddComponent<LineRenderer>();
        lr0.gameObject.transform.SetParent(transform);
        lr0.gameObject.transform.SetPositionAndRotation(Vector3.zero, Quaternion.identity);

        lr1 = new GameObject().AddComponent<LineRenderer>();
        lr1.gameObject.transform.SetParent(transform);
        lr1.gameObject.transform.SetPositionAndRotation(Vector3.zero, Quaternion.identity);

        lr2 = new GameObject().AddComponent<LineRenderer>();
        lr2.gameObject.transform.SetParent(transform);
        lr2.gameObject.transform.SetPositionAndRotation(Vector3.zero, Quaternion.identity);

        startRotation = Quaternion.Euler(0f, 0f, 0f);
        startPosition = Vector3.zero;
        startDQ = DualQuat.FromPose(startRotation, startPosition);

        endPosition = new Vector3(-10f, 10f, 10f);
        endRotation = Quaternion.Euler(180f, 0f, 0f);
        endDQ = DualQuat.FromPose(endRotation, endPosition);

        counter = 0;

        transform.position = startPosition;
        transform.rotation = startRotation;
    }

    private void FixedUpdate() {
        if (counter < totalFrames) {
            counter += 1;
            // interpolation
            var dq = DualQuat.Interpolate(startDQ, endDQ, (float)counter / totalFrames);
            DualQuat.ToPose(dq, out var rotation, out var position);
            transform.rotation = rotation;
            transform.position = position;

            // visualization
            DualQuat.ToScrew(endDQ, out var theta, out var axis, out var d, out var moment);
            var p = Vector3.Cross(axis, moment);
            var pStart = p - 20 * axis;
            var pEnd = p + 10 * axis;

            List<Vector3> line0 = new List<Vector3> { startPosition, endPosition };
            lr0.startWidth = 0.1f;
            lr0.endWidth = 0.1f;
            lr0.SetPositions(line0.ToArray());

            List<Vector3> line1 = new List<Vector3> { pStart, pEnd };
            lr1.startWidth = 0.1f;
            lr1.endWidth = 0.1f;
            lr1.SetPositions(line1.ToArray());

            Vector3 temp = position - pStart;
            var offset = Vector3.Dot(temp, axis);
            var shortestIntersect = pStart + offset * axis;
            List<Vector3> line2 = new List<Vector3> { position, shortestIntersect };
            lr2.startWidth = 0.1f;
            lr2.endWidth = 0.1f;
            lr2.SetPositions(line2.ToArray());

            var distance = Vector3.Distance(position, shortestIntersect);
            Debug.Log($"Distance to screw axis [{distance}]");
        }
        
    }
}

Full script: MoveDQ.cs

Underlying Maths for ScLERP with Dual Quaternions

Quaternion

Quaternion, q=(u0,u)q = (u_0, \mathbf{u}), where u0∈Ru_0 \in \mathbb{R} and where u∈R3\mathbf{u} \in \mathbb{R}^3.

or more explicitly,

q=u0+u1i^+u2j^+u3k^q=u_0 + u_1 \mathbf{\hat{i}} + u_2 \mathbf{\hat{j}} + u_3 \mathbf{\hat{k}}

In Unity convention,

var q = new Quaternion(x:u1,y:u2,z:u3,w:u0);

Quaternion product

The product of two quaternions satisfies these fundamental rules introduced by Hamilton,

i^2=j^2=k^2=i^j^k^=−1\mathbf{\hat{i}}^2 = \mathbf{\hat{j}}^2 = \mathbf{\hat{k}}^2 = \mathbf{\hat{i}}\mathbf{\hat{j}}\mathbf{\hat{k}} = -1

i^j^=k^=−j^i^\mathbf{\hat{i}}\mathbf{\hat{j}} = \mathbf{\hat{k}} = -\mathbf{\hat{j}}\mathbf{\hat{i}}

j^k^=i^=−k^j^\mathbf{\hat{j}}\mathbf{\hat{k}}=\mathbf{\hat{i}} = -\mathbf{\hat{k}}\mathbf{\hat{j}}

k^i^=j^=−i^k^\mathbf{\hat{k}}\mathbf{\hat{i}}=\mathbf{\hat{j}}=-\mathbf{\hat{i}}\mathbf{\hat{k}}

Product of 2 quaternions p=(u0,u)p=(u_0, \mathbf{u}) and q=(v0,v)q=(v_0, \mathbf{v}) is defined as

pq=(u0,u)(v0,v)=(u0v0−(uTv),u0v+v0u+u×v)pq = (u_0, \mathbf{u})(v_0, \mathbf{v}) = (u_0v_0 - (\mathbf{u}^T\mathbf{v}),u_0\mathbf{v}+v_0\mathbf{u} + \mathbf{u} \times \mathbf{v})

Quaternion conjugate

For q=(u0,u)q = (u_0, \mathbf{u})

Quaternion conjugate, q∗=(u0,−u)q^* = (u_0, -\mathbf{u})

Representing rotation with unit quaternion

Rotation around an axis, w^\mathbf{\hat{w}} by an angle θ\theta, where ∣∣w^∣∣=1||\mathbf{\hat{w}}|| = 1 can be represented by a unit quaternion

qrot=(u0,u)=(cos⁡θ2,sin⁡θ2w^)q_{rot} = (u_0, \mathbf{u}) = (\cos \frac{\theta}{2}, \sin \frac{\theta}{2}\mathbf{\hat{w}})

Dual quaternion

q^=qr+εqd\hat{q} = q_r + \varepsilon q_d,

where

qr=(ur,ur)q_r = (u_r, \mathbf{u_r}), real part

qd=(ud,ud)q_d = (u_d, \mathbf{u_d}), dual part

ε2=0,ε≠0\varepsilon^2 = 0, \varepsilon \neq 0

Dual quaternion product

Product of 2 dual quaternions p^\hat{p}, and q^\hat{q} is defined as

p^q^=(pr+εpd)(qr+εqd)\hat{p}\hat{q} = (p_r + \varepsilon p_d)(q_r + \varepsilon q_d)

p^q^=prqr+ε(prqd+pdqr)+ε2pdqd;ε2=0\hat{p}\hat{q} = p_rq_r + \varepsilon (p_rq_d + p_dq_r) + \varepsilon^2 p_dq_d \quad;\varepsilon^2 = 0

p^q^=prqr+ε(prqd+pdqr)\hat{p}\hat{q} = p_rq_r + \varepsilon (p_rq_d + p_dq_r)

Dual quaternion conjugate

For q^=qr+εqd\hat{q} = q_r + \varepsilon q_d,

Dual quaternion conjugate, q^∗=qr∗+εqd∗\hat{q}^* = q_r^* + \varepsilon q_d^*

where qr∗q_r^* and qd∗q_d^* are quaternion conjugates for real and dual part respectively.

Representing rigid transformation with dual quaternion (rotation + translation)

q^=(cos⁡θ2,w^sin⁡θ2)+12ε[(0,t)(cos⁡θ2,w^sin⁡θ2)]\hat{q} = (\cos \frac{\theta}{2}, \mathbf{\hat{w}}\sin \frac{\theta}{2} ) + \frac{1}{2}\varepsilon [(0, \mathbf{t})(\cos \frac{\theta}{2}, \mathbf{\hat{w}}\sin \frac{\theta}{2} )]

where translation, t=[tx,ty,tz]T∈R3\mathbf{t} = [t_x,t_y,t_z]^T \in \mathbb{R}^3

q^=qrot+12ε(qtransqrot)\hat{q} = q_{rot} + \frac{1}{2}\varepsilon (q_{trans}q_{rot})

Representing rigid transformation with dual quaternion (screw)

The elements of a unit dual quaternion are related to the screw parameter of a 3D rigid transformation as:

q^=(cos⁡θ2,w^sin⁡θ2)+ε(−d2sin⁡θ2,Msin⁡θ2+w^d2cos⁡θ2)\hat{q} = (\cos \frac{\theta}{2}, \mathbf{\hat{w}}\sin \frac{\theta}{2} ) + \varepsilon (-\frac{d}{2}\sin \frac{\theta}{2}, \mathbf{M} \sin \frac{\theta}{2} + \mathbf{\hat{w}}\frac{d}{2}\cos \frac{\theta}{2})

where

w^\mathbf{\hat{w}} is the screw axis, with w^∈R3\mathbf{\hat{w}} \in \mathbb{R}^3 and ∣∣w^∣∣=1||\mathbf{\hat{w}}|| = 1.

M\mathbf{M} is the moment of the screw axis w.r.t. the origin, with M∈R3\mathbf{M} \in \mathbb{R}^3.

θ\theta is the screw angle

dd is the screw translation

Power of a dual quaternion

q^h=[cos⁡(hθ2),sin⁡(hθ2)w^]+ε[−hd2sin⁡(hθ2),Msin⁡(hθ2)+w^hd2cos⁡(hθ2)]\hat{q}^h = [\cos (\frac{h\theta}{2}), \sin (\frac{h\theta}{2})\mathbf{\hat{w}}] + \varepsilon [-\frac{hd}{2}\sin (\frac{h\theta}{2}), \mathbf{M}\sin (\frac{h\theta}{2}) + \mathbf{\hat{w}}\frac{hd}{2}\cos (\frac{h\theta}{2})]

Dual quaternion interpolation

ScLERP interpolates between two unit dual quaternions q^1\hat{q}_1, q^2\hat{q}_2 with parameter h∈R∈[0,1.0]h \in \mathbb{R} \in [0, 1.0]

ScLERP(q^1,q^2,h)=(q^2q^1∗)hq^1(\hat{q}_1,\hat{q}_2,h) = (\hat{q}_2\hat{q}_1^*)^h\hat{q}_1

References

  1. Yan-Bin Jia: Dual Quaternions.
  2. Daniilidis, Kostas. “Hand-Eye Calibration Using Dual Quaternions.” The International Journal of Robotics Research 18 (1999): 286 - 298.
  3. Kavan, Ladislav et al. “Dual Quaternions for Rigid Transformation Blending.” (2006).